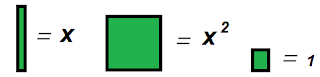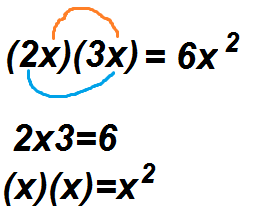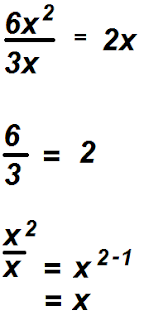So there are 18 red marbles. Now you fill in x will 18 to find out how many green marbles there are in the bag.
Scribe Post for April 28, 2010
So there are 18 red marbles. Now you fill in x will 18 to find out how many green marbles there are in the bag.
Karen's Journal Entry
February 23, 2010
So today, Mr. Backe gave us questions to identify the number of terms, name and degree of an expression like this:
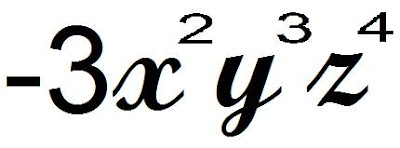
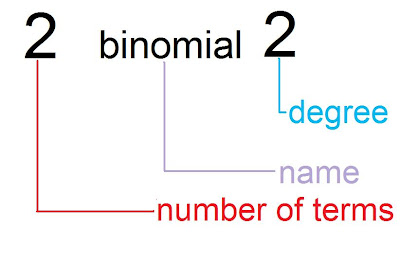
I think it's pretty easy but he let's us practice because he wants to make sure that we all get it because this stuff is important. He also mentioned polynomials being part of what we need for Grade 10 especially for people taking Pre-Cal. He' going to be talking more and more about it and he's going to teach us "fun" Grade 10 stuff. I never found Math "fun" but maybe it will be. He also made us do matching words (match words and definition). It was really easy because all of the words were in my notes and I know almost all of them except for like terms, terms that only differ only by their numerical coefficients. After, he assigned us assignments, questions from the textbooks, and then he stopped talking and let us do our own work, quietly. I wasn't quiet and he knows that...I finished 5 questions though (:
It's hard for me to do work in class, I need a silent environment and plus and get distracted easily.
Scribe for April 26
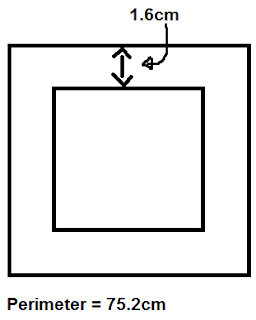
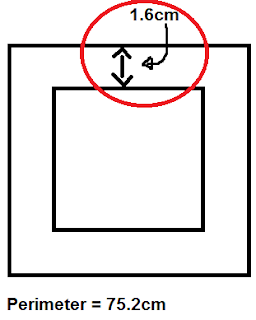
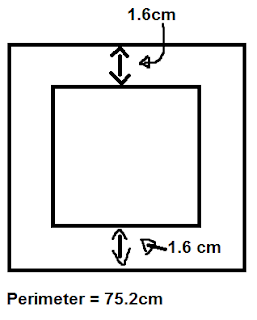
Once you get your answer which is 3.2, you have to divide 75.2 (perimeter) by 4 so you could get the side length each side of the outside of the frame. You want to do this because if you multiply 3.2 (width times 2) by the side length of the outside which 18.2 you will get the side length of the inside square.
Did you get an answer of 15.6? Well if you did then you have got the right answer.
After solving that question we went onto question 27 also in section 8.3 (textbook) which was even difficult for Mr. Backe to solve. Well here is the question...
Tahir is training for an upcoming cross-country meet. He runs 13 km, three times a week. His goal is to increase his average speed by 1.5 km/h, so that he can complete each run in 1 1/4. How long does he take to complete each run now, to the nearest tenth of a minute. Solve this problem in two different ways.
Well I am not really sure how to solve this but this is what Mr.Backe did.

Thats all for today and sorry it is so late. Bye.
Scribe Post April 22, 2010
Read Pages 314 - 318
Check Your Understanding #4
Practise # 6-11
Apply # 12-22
Extend # 23-27
8.3 Workbook
MathLinks 8.1, 8.2, 8.3
Nicky's Journal Entry

Note: The above is a picture because I didn't realize that blogger doesn't allow copy/pasting from word. Also, click the picture to make it larger.
Alyanna's Journal Entry :)
Anyways .. I will talk about something in Chapter 6. This is coming straight from my journal. When you read it dont make fun of me -_-" I talk as if my journal is a diary.. LOL. So here it goes :)
Today in class, Backe asked if we have any questions or anything. No one did suprisingly.. The class was so quiete.. It was amazing. Well after that, he started talking about some patterns and things. Well there went the class.. We were talking about some pictures or something. Wait i'll show you. Just wait let me draw it :)
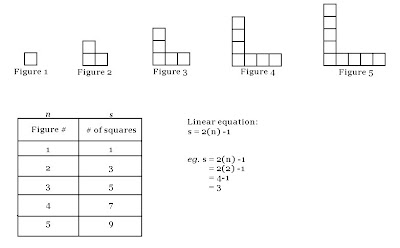
See this is what we are learning. We have to find out what the how many squares are in the fourth and fifth figure and the "linear equation" or something. Well yeah, I'm so lost.. Like you don't even understand.. But wait, I'll ask questions BE RIGHT BACK.
Okay I'm back.. Hey there! Well my questions helped me, I get it know ! yay me :) I'm going to go do it on my loose leaf! Bye Journal :) I wrote a lot in you today ! yay me :)
Scribe April 19, 2010
One of the questions he gave us too solve is....
ax+b=c .
I cant really show how to work it out but what you do is divide both by "A" and minus "C" by "B".
it should look like this...
ax=c-b
__ __ x=c-b
a . a . __
. a
The dots are here^^ because I can't move it over without anything there.
Sorry if its really bad!
Casey's Journal Entry March 22, 2010

Vikram's Journal Entry
Liem's Journal Entry
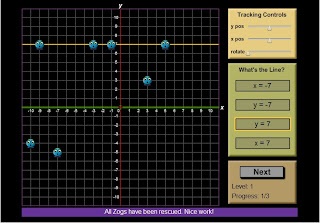
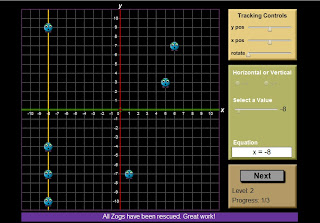
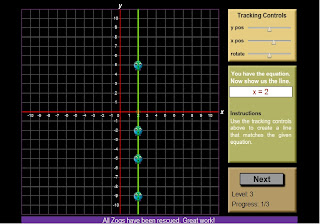
Today in class, we had a bit of fun! We played Save the Zogs, on www.mathplayground.com
Here's what we had to do :
" To rescue the Zogs, you need to learn as much as possible about linear equations and the lines they create. What happens when the slope is zero? What effect does the y intercept have the position of the line? The more you know, the more Zogs you can save! "
So basically, we had to find linear equations, in order to save the Zogs. Also after passing a few levels of the game, the game involves finding the x, y position and rotation of the line. This game is very fun, but involves math which was very interesting. I really liked how the game wasn't too hard to play but was very fun. I really learned a lot from this game, its awesome. That's what we did today!
Here are some screen shots :

Abby's Math Journal Entry
Today in math class, we took notes for Chapter 6. We learned about linear relations and linear equations. I learned that a linear relation is a relation that is in a straight line when graphed. We worked on a pictorial pattern. It was kind of hard to understand at first, but when Mr. Backe explained it, it was easy. This is what we worked on in math class:
Kim's Math Journal Entry
Todayin room 5 for math, we went on the website http://www.mymathplayground.com(that/ I didn't go on due to somethings... >.>) and played rescue the zongs.
Just by doing it you can learn A LOT!
For example:
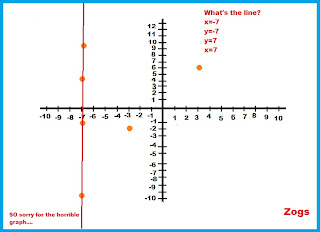
I learned that if the line is vertical like the y axis, it is an "x" line and if it's a horizontal line like the x axis. then it is a "Y" line.
I also learned that you can make a chart to find out the answer.
For example:
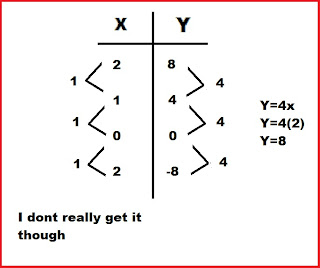
Tracey's Journal Entry
We went over some questions in math class. Different colours indicate different questions


Melanie's Journal Entry
Today we went over the assigned homework, which one of the questions were number 17, on page 197 in the textbook. The "Addition Pyramid." At first I was confused, but the more we discussed it as a class, the more I understood. It's all about "combining like terms."
Here's the question:
17. Complete the addition pyramid. Find the value in any box by adding the expressions in the two boxes immediately below it.
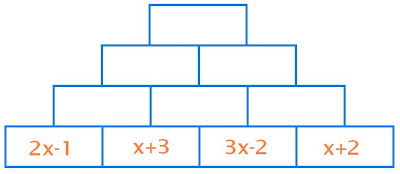
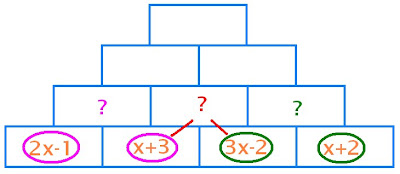
Do you get the pattern?
So ...
first the pinkish purplish:
2x-1+x+3
= 3x+2
second the dark green:
3x-2+x+2
= 4x
third both of them combined:
x+3+3x-2
= 4x+1
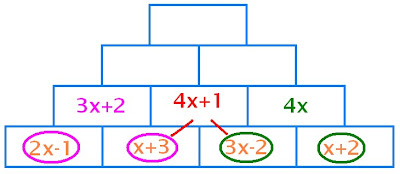
That's all for my journal entry. Thanks for reading (:
Brendan's Journal Entry
Today in math we learned how to divide polynomials using algebra tiles.
Then we were given another question about dividing polynomials, It was about a cylinder and what the ratio of the Surface area to the radius was.
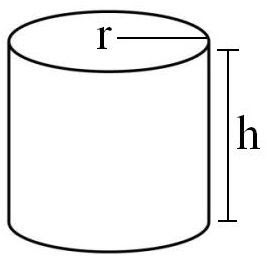
To figure out this question you need to know the formula for a cylinder.
The formula is:
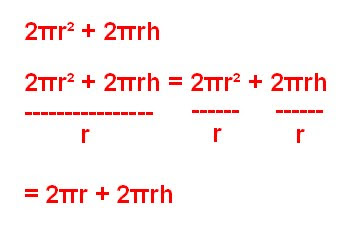
At the end of class class we were given homework to do. While we were working Mr. B told us what he wanted in our stash its.
(Chapter 5 & 7 work)
Krissia's Journal Entry
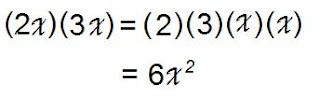
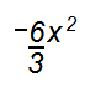
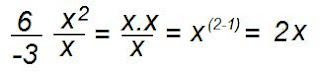
Shaneille's Journal Post
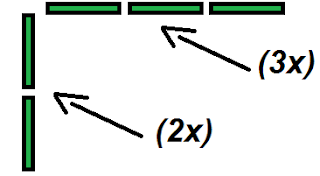
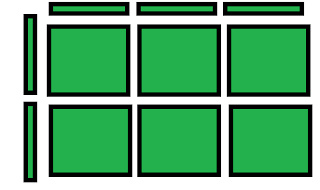
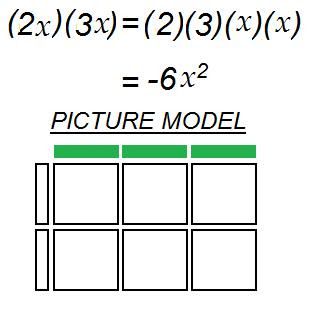
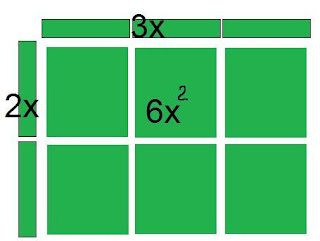(3x).jpg)
(2x)(3x)
which means (2)(3)(x)(x)
(2)(3) =6
(x)(x) = x^2
So (2x)(3x)=
=6x^2
Then dividing.
6x/-3x = -2x

Christian's Journal Entry
Today in math, we analyzed the difference between Extrapolation and Interpolation, we also differentiate, Linear Relation and Linear Equation...
INTERPOLATION: Estimating a value between the given value.
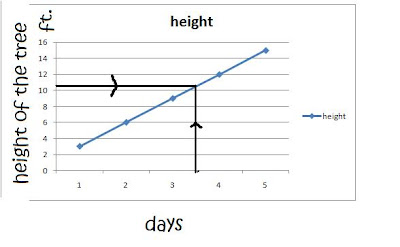
EXTRAPOLATION: Estimating a value beyond the given value.
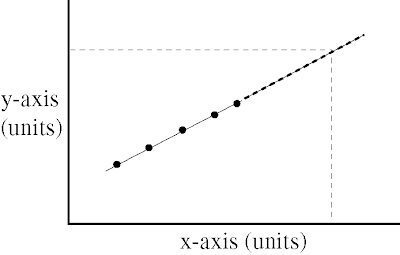
Linear equation is finding the equation on the x and y axis, showing a straight line when graphed.
Example.
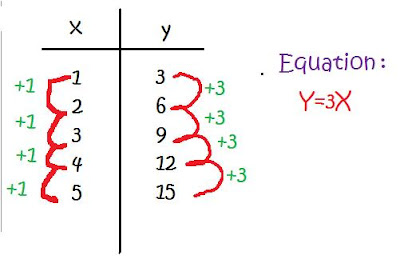
Linear relation is relation that appears as a straight line whe
Kristin's Journal Entry
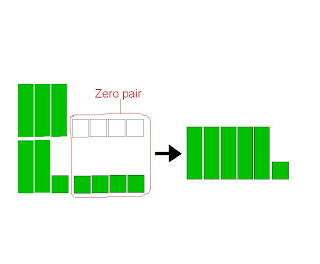 - use symbols
- use symbols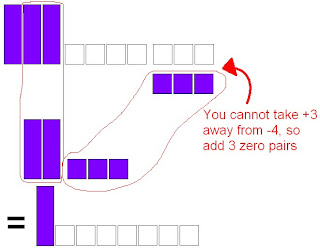
- add the opposite
(3x - 4) - (2x + 3)
= (3x - 4) + (-2x - 3)
= 3x - 2x -4 - 3
= x - 7
Jounel Entry Post