Abby's Math Journal Entry

2010 03 23

Today in math class, we took notes for Chapter 6. We learned about linear relations and linear equations. I learned that a linear relation is a relation that is in a straight line when graphed. We worked on a pictorial pattern. It was kind of hard to understand at first, but when Mr. Backe explained it, it was easy. This is what we worked on in math class:

Scribe Post for April 6, 2010

Hey 9-05! Abby here with today's scribe post! Okay let's get started!

Okay so in the beginning of math class, Mr. Backe explained on how to do the 6.1 Math Link.

1. a) Choose one of the following regular polygons for a race course.





So for 1. a), all you have to do is choose one of the polygons. You can choose the triangle, or the square, or the rhombus, or the pentagon. It doesn't matter what you choose, as long as it's one of the four regular polygons!
For an example, I will choose a square.








1. b) Draw and label the five race courses.

• Decide on the length of the side of the first course. (It mus be at least 5 km long.)
• Decide on the length of the sides of the last course. (The longest course must be no longer than 35 km.)
• Decide on the length of the sides of the other courses.
• [!] Each length must be a whole number because the figure numbers are whole numbers.
  

So for 1. b), the regular polygon you chose will become 5 race courses. Since we are using the square for an example.. (sorry for the small picture!)







So, we put course #1, 2, 3, and 4 inside course #5.













And then, we choose a length for the first course. So lets use.. 2 as the length for the first course.














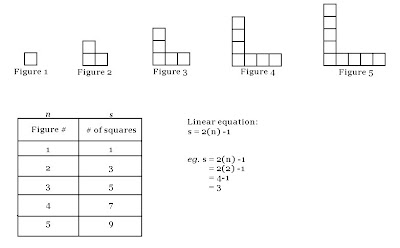
For the second course, the length would be 3 since the second course is larger than the first course. For the third course, the length would be 4, the fourth course would have a length of 5, and the fifth course would have a length of 6.

2. Develop a linear relation that describes the race courses. a) Complete the first two columns in the table of values.
(I'm not going to show the pattern part, just the first two columns)
















So when you have the second column filled out, find out the pattern by multiplying n by __ which will be the numerical coefficient, and add ___ which will be the constant.

So for the rest of the class, we worked on our 6.2 homework.
___________________________________________________

So that ends my scribe post for April 6, 2010! I hope I explained the 6.1 Math Link stuff well. If there are any errors, or something doesn't make sense, please comment! Have a goodnight 9-05! :D

The Spiral Rational Game

The Spiral Rational Board Game Rules.

RED SPACES - Go back on space
BLUE SPACES - Pick up a card

GREEN SPACES - Go forward one space

Cards
- When you land on a blue space, someone (it could be anyone of the players) picks up a card and reads it to you, then you have to answer. If you got it wrong, you miss a turn, and if you got it correct, you are safe until your next turn.

How to start
- To start a game, you have to choose which colour cone you want to be. (UP TO 4 PLAYERS). To choose who goes first, each person gets to roll the die, whoever gets the highest gets to go first and the second person is the person who got the second highest and so on. The winner is the person who has reached to the finish line before everyone else.

To Mr. Backe

Hello Mr. Backe! How are you doing? I hope you are doing well! We miss you a lot! Math class is different without you! Thank you, for being such a kind and awesome teacher to us. You're always there when we need help and I am very thankful for that! Thank you for giving us chocolates too! (: Anyways, I would like to wish you a very Merry Christmas and a Happy New Year~! See you next year Mr. Backe! :D

Here is a picture I drew for you!

Multiplying Decimals

Hey 9-05! Abby here with a blog post about multiplying decimals! Multiplying decimals may seem hard, but it's fairly easy!

So let's work with these numbers:







So first of all, you have to multiply 5 by each individual number in 13.33.









Then, you multiply 6 by each individual number in 13.33. You have to add a zero at the end because you're actually multiplying by tenths.









Next, you multiply the 7 by each individual number in 13.33. Then, add two zeros to the end.













Now, what you have to do is add the answers up.














Oh! But we're not done yet! Since each factor contains a decimal, then the product must contain a decimal too! But how do we know where to put it? All you have to do is count how many numbers there are behind the decimals.













So since there are 4 numbers behind the decimals, we change the place value of the decimal 4 place values to the left.















So 13.33 multiplied by 7.65 gives a product of.. 101.9745!













_____________________________________________________________

So that's my post about multiplying decimals! I hope I explained this well! If there are any errors, or you don't understand anything, please feel free to comment! Thanks for reading guys! Have a good evening 9-05!

Question #10

Hello 9-05! Abby here with question number 10! Okay so let's get started!

A carpenter has 64 m of baseboard. He installs 1/2 of the baseboard in one room. He installs another 3/5 of the original amount of the baseboard in another room. How much baseboard does he have left?


So first, we have to multiply 64 by 1/2 because we want to find out how much of the baseboard the carpenter used in the first room. Here's how it goes:














The carpenter used 32 m of the baseboard for the first room.


Because the question says he used another 3/5 of the original amount (64), we just have to multiply 64 by 3/5 to find out how much of the baseboard the carpenter used in the other room using the original amount.

















For this equation, I used a calculator to convert 38 and 2/5 to 38.4. So the carpenter used 38.4 m of the baseboard in the other room.


Now, we have to add the amount of baseboard the carpenter used in the first room (32) and the amount of baseboard the carpenter used in the other room (38.4). We have to do this because this will be a part of finding what the carpenter has left.





Then, we have to get the original amount of the baseboard (64) and subtract the amount of baseboard that was combined from the two rooms the carpenter used (70.4). This will help us find what the carpenter has left.





The answer is -6.4 m! Since the answer is negative, it means the carpenter needs or is short on baseboard.


So the word problem sentence would be..

The carpenter needs 6.4 m of baseboard.
___________________________________________________

Well, that's my blog post for question number 10! If there are any errors, and if you don't understand something, please feel free to comment! I will try my best to change my post to make you guys understand it better! Anyways, have a great weekend 9-05! (:

Question #13

Hey 9-05! Abby here with Question #13! Okay then.. let's start!

A submarine was cruising at a depth of 153 m. It then rose at 4.5 m/min for 15 min.














































I wanted to make the submarine yellow, because I wanted The Beatles to live in it! Haha. Isn't that a funny joke? Or did I just kill the moment? Haha. Anyways..

a) What was the submarine's depth at the end of the rise?
To answer this question, you first have to find how much meters the submarine goes up in 15 mins. So to do this, you have to multiply 4.5 by 15, which comes to 67.5.

4.5(15) = 67.5

Then, you have to add -153 to 67.5. The 153 meters is negative because it's below sea level.

67.5 -153 = -85.5

Then, you have to convert -85.5 into 85.5 because the submarine is going up.

-85.5 --> 85.5

The submarine's depth at the end of the rise is 85.5 m.


b) If the submarine continues to rise at the same rate, how much longer will it take to reach the surface?
To answer this question, all you have to do is divide the submarine's depth at the end of the rise by how much meters you go up a minute. So that becomes..

85.5/4.5 = 19

The submarine will take 19 minutes longer to reach the surface.
_______________________________________________________________

I hope my new explanations made you readers unconfused! If there are any errors in grammar, math equations, and if it still doesn't make sense, please feel free to comment and I'll try my best to make it better..er. Haha. Have a wonderful weekend 9-05! ;D

Scribe Post for October 27, 2009

Hey 9-05! Abby here with today's scribe post! First of all, I'd like to congratulate us 9-05 people. I think we did a really good job on the blog posts we've been doing.. So let's keep it up!

Okay, so today in math class, we went to the computer lab. First, we went over our homework from yesterday. I think some of us had a hard time with finding a fraction for a repeated decimal number with 3 numbers after the decimal. So here is the rule:













For this rule, you always want to multiply out all the repeating. So 0.2 repeated has to be multiplied by 10 to move the decimal down 1 place value. 0.43 repeated has to be multiplied by 100 to move the decimal down 2 place values, and 0.172 repeated has to be multiplied by 1000 to move the decimal down 3 place values.

x = o.2 (repeated)
10x = 2.2
9x/9 = 2/9
x = 2/9

x = 0.43 (repeated)
100x = 43.43
99x/99 = 43/99
x = 43/99

x = 0.172 (repeated)
1000x = 172.172
999x/999 = 172/999
x = 172/999


After that stuff, the people who needed help with the chessboard question went to the hallway with Mr. Backe so he could explain it to us. Here, I will explain and show you how to start the chessboard question.

1. A chessboard is a large square and is made up of 64 small squares. Consider only the first three rows of the chessboard.

a) Find the diagonals of all squares and rectangles possible in the first three rows. Arrange the squares and rectangles, from least to greatest, by length of their diagonals.

So first, we look at the first square on the chessboard:

Figure 1.0
















So, to find the diagonal for square number one, we have to use the a²+b² = c² formula. For the square, the dimensions are 1 by 1.

This is how you find the diagonal for square number one:
a²+b² = c²
1²+1² = c²
1+1 = c²



1.414 = c


Now, I'll show how to do the second part:

Figure 1.1















For the second square, we use the exact same formula, but the number change. B changes into 2 because the sides, which are all equal, are 1. And so, 1 side + 1 side = 2 sides. Or, to make easier 1+1=2!:
a²+b² = c²
1²+2² = c²
1+4 = c²



2.236 = c

Then, we have to do the rest of row number 1, which is the same procedure. When you go up one square, the b changes because the number of bottom sides are adding up. The a stays the same, and the hypotenuse grows larger. (I'm not sure if I made sense there..)

Figure 1.2







(sorry if the image is blurry!)


The second row has the same procedure except for the first diagonal because we already figured it out in row 1! (refer to Figure 1.1)

Figure 1.3











The third row ALSO has the same procedure except for the first diagonal because, like the second row, we already figured the first diagonal for the third row in row 1 (refer to Figure 1.1)

Figure 1.4









For the rest of the class, we went on mathlinks9.ca and shodor.org. In Mathlinks9.ca, we checked out some websites under student center; chapter 2; weblinks. Also, Mr. Backe told us to read a bit about Neil Barlett. On shodor.org, we did some games on fractions.

HOMEWORK:
-play some fraction games on shodor.org
-fill in math journal

Thanks for reading! If there's anything on here that doesn't make sense, or seems wrong, please comment and I'll try my best to correct my mistakes! Okay everyone, have a good evening!

The next scribe I choose for tomorrow is.. Nicky!

Elegant Algebraic Expressions

First of all.. I'd like to say HAPPY THANKSGIVING/TURKEY DAY to everyone! (: Okay so this blog post will be about the most elegant algebraic expressions to help you find the surface area for a cube, a rectangular prism, a cylinder, and a composite shape. So let's start! :D


What is the most elegant algebraic expression for a cube?
The most elegant algebraic expression for a cube is 6s².

So now, we'll use a 2 by 2 cube for an example to find the surface area.















This is how you find the surface area for a cube: S.A. of cube = 6s²
S.A. of cube = 6(2²)
S.A. of cube = 6(4)
S.A. of cube = 24u²


What is the most elegant algebraic expression for a rectangular prism?
The most elegant algebraic expression for a rectangular prism is 2(lw)+2(hw)+2(lw).

For an example, we'll use a rectangular prism with a length of 5, a width of8, and a height of4.















This is how you find the surface area for a rectangular prism:
S.A. of rectangular prism = 2(lw)+2(hw)+2(lw)
S.A. of rectangular prism = 2(5x8)+2(4x8)+2(5x8)
S.A. of rectangular prism = 2(40)+2(32)+2(40)
S.A. of rectangular prism = 80+64+80
S.A. of rectangular prism = 224cm²


What is the most elegant algebraic expression for a cylinder?
The most elegant algebraic expression for a cylinder is 2πr²+2πrh.

To show how to find the surface area of a cylinder, we'll use a cylinder with a diameter of 10 and a height of 15.














This is how you find the surface area for a cylinder:
d/2 = r
10/2 = r
5 = r

S.A. of cylinder = 2πr²+2πrh
S.A. of cylinder = 2π5²+2π5(15)
S.A. of cylinder = 2π25+2π75
S.A. of cylinder = 50π+150π
S.A. of cylinder = 157.079+471.238
S.A. of cylinder = 628.317u²

What is a composite figure?
A composite figure is a figure or shape that can be divided into more than one of the basic figures.

Here is an example of a composite figure:
This figure is divided into two squares and triangles, which are basic shapes.










How does symmetry help us solve some of these surface area problems?
Symmetry helps us solve these surface area problems because if you know a shape has symmetry you would that it is balanced. Like a rectangle.. it's front is the same as it's back, and so as the 2 sides and the top and bottom. I'm not sure if I made sense here though.

OKAY.. So I hope this blog post helped anyone who needed help! If there's anything missing, or if there's any errors, don't be afraid to comment~! Have a good Thanksgiving/Turkey Day you guys and I'll see you tomorrow~!

Why 360?

Why, why, why is a full circle called 360 degrees? Well.. It all started with the Babylonians.

For the Babylonians, counting was based on a Sexagesimal System, or a base of 60. The Babylonians would have symbols for the numbers 1 t0 59, and when they got up to 60, they would combine those symbols to make the number 60.

Here is what the symbols looked like:















Another reason why we call a full circle 360 degrees is because the Babylonians had a calendar that consisted of 360 days. The earth takes about 360 days to rotate all around the sun.
























ALSO, the number 360 is very convenient. The number 360 is able to be divided by a lot of different numbers such as 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, and 15.

I hope you guys learned something from my blog post! If you see any errors or have any suggestions, there's a comment button waiting for you! Thanks for reading~!