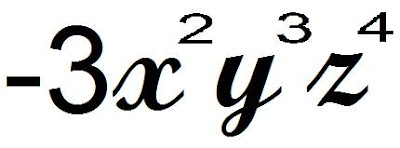Karen's Journal Entry

Note: I'm sorry for the super late post Mr. Backe and class, my computer got a virus and was sent to be fixed last Monday and I just got it back today so I am really, really sorry.

February 23, 2010

So today, Mr. Backe gave us questions to identify the number of terms, name and degree of an expression like this:




















I think it's pretty easy but he let's us practice because he wants to make sure that we all get it because this stuff is important. He also mentioned polynomials being part of what we need for Grade 10 especially for people taking Pre-Cal. He' going to be talking more and more about it and he's going to teach us "fun" Grade 10 stuff. I never found Math "fun" but maybe it will be. He also made us do matching words (match words and definition). It was really easy because all of the words were in my notes and I know almost all of them except for like terms, terms that only differ only by their numerical coefficients. After, he assigned us assignments, questions from the textbooks, and then he stopped talking and let us do our own work, quietly. I wasn't quiet and he knows that...I finished 5 questions though (:
It's hard for me to do work in class, I need a silent environment and plus and get distracted easily.

Scribe Post for April 5, 2010

HELLO PEOPLES!! :D Spring Break is finally over, Monday first day back to school (:
how was your Spring Break 9-05? Did you do homework assigned for us over the break? I know...I didn't do it either..I did half (: I hope you guys had a good break though.
k, so first day back to school and we got homework assigned for us already..

• 6.2 workbook
• 6.2 Extra Practice
• 6.2 Textbook
• SYK page 223, 225
• Read Key Ideas
• CYU page 226 #1, place in foldable
• Practise # 4 or 6, 7, 8 or 9 or 10, 11
  
• Apply: ALL
• Extend 18 or 19
• Mathlink page 230 in foldable (use Mathlink handouts for help

ALL DUE Thursday, April 8.
There's possibly a test next week, just reminding everybody! :D

Make sure you guys also did our past homework: ALL OF 6.1 STUFF, so you're caught up.

So we didn't really do anything in class today, we just did questions that we didn't really understand. There were only two:
Check Your Understanding #2:












and Extend #16













I'd explain and review everything but I don't have time, I'm sorry. You guys probably got in class today.

So quick review to freshen up everybody's minds:
Chapter 6: Linear Relations
6.1 - Representing Patterns

Quick Overview...





















I'm sorry I didn't really help. I really don't have time to review the 2 questions and make a better overview of what we're learning.

Scribe Post for January 7, 2010

Hello 9-05 ! So today we started Chapter 3.2: Exponent Laws. Mr. Backe helped us with some stuff we didn't understand in our homework yesterday:

• Read page 99 to 104
• Answer Explore Operations on powers, Reflect and Check, Check Your Understanding- page 105, and all Show You Knows-page 101, 102, 103 and 104.

In class, we wrote notes in our foldables.







































We wrote notes in the middle where it says Exponent Laws and Key Words.

FIRST FLAP:



The Product Law:
When multiplying powers of the same base, simply add the exponents to find the product
example:


We also had to put not examples, exponents with different bases:


SECOND FLAP:



The Quotient Law:
When dividing powers of the same base, simply subtract the exponent to find the quotient.
example:


We also had to put not examples, exponents with different bases:

THIRD FLAP:


The Power of a Power Law:
When raising a power by a power, simply multiply the exponents to find the new power.
example:


WHY? it's because this question means to multiply 5 x 5 3 more times.

FOURTH FLAP:


Power of a Product Law:
When a product is raised to an exponent, you can rewrite each number in the product with the same exponent.
example:

FIFTH FLAP:


Power of the Quotient Law:
When a quotient is raised to an exponent, you can rewrite each number in the quotient with the same exponent.
example:


SIXTH FLAP:


The Zero Exponent Law:
When the exponent of a power is 0. The value of the power is 1 if the base is not equal to 0.
example:


WHY? It is 1 and a positive even though the base is a negative because it fits the pattern. Watch...



See what's happening? This reminds me of the rule about multiplying and dividing integers:

*When multiplying or dividing variables, if there's an even amount of positive or negative numbers the answer will be a positive.

*When multiplying or dividing variables, if there's an odd amount of positive or negative numbers the answer will be a negative.


Homework:

• Practise, Apply and Extend - Odd or Even numbers.
• 3.2 Extra Practice
• 3.2 Workbook
• Fill in definitions and examples for 3 point approach and foldable so you're caught up with everything
• Self Assessment for 3.1 and 3.2 since we're done both
• JOURNAL
  
• also try to figure out definition of Exponent Law of 1, Negative Exponent Law, Base of 1 Law if you have time (:

Extra Info you guys may need in case it pops up in the homework:
Negative Exponents: I think it's the same as Negative Exponent Law..I'm not sure.


If a positive exponent means how many times you multiply the base by itself, a negative exponent means how many times you divide the base by itself.


Please comment and tell me what you think, point out my errors and things I could improve on (:

Dear Mr. Backe (:

hello (: karen here! how are you Mr. Backe? i hope you're doing fine... and condolence ): it's sad that this happened. since we won't see you until after Christmas break i can't wish you a merry Christmas and a happy new year in person. i hope you get through this and we really hope we could see you tomorrow - last day- so we can all give you a big hug. we REALLY miss you, math class is different without Mr. backe making fun of everyone and teaching us new things. you are a great teacher and you've already taught us a lot of things not just about math. you have dedicated soo much time and effort to help us and make us better students. you were there for us to help and we will do the same for you(: we really wish you can come back sooner but we know that you need time, i hope you still enjoy your Christmas. we can't wait to see you next year (:

MERRY CHRISTMAS AND A HAPPY NEW YEAR! :D

Re-Made Rational Number Video

Well guys, since the video Joseph posted many weeks ago had a bit of problems, Karen, Linda and I decided to fix it up. However, being what society is today, we put it off quite some bit. So sorry if it's hard to understand, or if the voice is a bit off.



PLEASE comment. Constructive criticism is always welcome. I'm pretty sure we also had some mistakes in there, but hey, nothing is ever perfect.

a.) The question is asking for how many hours St. John's is ahead of Brandon and to get the answer you have to find the difference of the time in St. John's and Brandon. In other much simpler words, you have to subtract it.
So the time in St. John's is -3 1/2 and the time in Brandon is -6, you have to subtract those two:
-3 1/2 - (-6) = -3 1/2 + 6/1

* now here comes the explaining part:
Why did it turn into a plus sign and where did the negative sign from the -6 go? and why is it 6/1 when it is only 6?

answer to those questions:
It turned into a plus sign and the negative sign from the 6 disappeared because it is now a positive number. When you have a question like this: a - (-b)=c, it is an "oopsie". I think it turns into a positive automatically because the question really is saying: a - 1 (-b)=c. So if you substitute those letters with numbers it will be like this:

-3 1/2 - (-6) = -3 1/2 -1 (-6)...... because of BEDMAS (order of operations) you have to get rid of the brackets first so you have to do -1 times -6 so it turns into +6.
Then it is 6/1 because mathematicians are lazy, they wrote 6 instead of 6/1 because they know that 6 and 6/1 are the same. It is just like the whole "oppsies" thing.

Now to solve it: - WOW that was a very long explanation -___- sorry guys.
-3 1/2 - (-6) = -3 1/2 + 6/1
= -7/2 + 12/2 (I just turned into an improper fraction because it is easier for me)
= 5/2 or 2 1/2 hours
St. John's is ahead of Brandon by 2 1/2 hours.

b.) The question is practically saying how many hours do you need to add to -8 to get to 5 1/2.
Here's a number line to make it easier (:

















There's 13 1/2 hours.

c.) This question is asking for the difference of the time in Tokyo and Kathmandu. So all you have to do is subtract it.
9 - (5 3/4) = 9/1 - (23/4)
= 36/4 - 23/4 (equivalent fractions. Least common denominator because it needs the same denominators)
= 13/4 or 3 1/4 hours
There's 3 1/4 hours time difference between Tokyo and Kathmandu.

d.) This question is also asking for the difference of the time in Chatam Islands and St. John's. You also have to subtract.
12 3/4 - (-3 1/2) = 51/4 + 7/2 ( if you're asking about this equation again look up to the first one, the very long explanation )
= 51/4 + 14/4
= 65/4 or 16 1/4 hours
There's 16 1/4 hours time difference between Chatam Islands and St. John's.

e.) The question is asking you what location has the same time as the difference of Istanbul and Alice Springs halfway. It is asking you to subtract The time in Istanbul, +2, from the time in Alice Springs, +9 1/2 then divide in to t2 because it says "halfway" then see what other location in the list has the same number.
(9 1/2 + 2) ÷2 = (19/2 + 2/1) ÷2
= (19/2 + 4/2) ÷2
= 23/2 ÷ 2/1
= 23/2 x 1/2 ( you have to multiply the dividend by the divisors reciprocal)
= 23/4 or 5 3/4 hours
Kathmandu, Nepal has the same time so Kathmandu, Nepal is the location that has the same time as the difference of Istanbul and Alice Springs halfway.


Sorry if I didn't explain it that well. I tried to explain it and make it as detailed as possible. I guess I just made it long and broing -___-. At least I tried and finished my work ! :D

Question #15

15.) In dry air, the temperature decreases by about 0.65 degrees Celsius for each 100 meter increase in altitude.

a.) The temperature in Red Deer, Alberta, is 10 degrees Celsius on a dry day. What is the temperature outside an aircraft 2.8 kilometers above the city.



The picture is not really clear I'm going to explain it:
a.) The answer is -8.2 degrees C at 2.8 km.
How did I get this? I added 10 degrees by negative 18.2 degrees.
How did I get -18.2
(0.65/100)x(2.8)x(1000)
*1 km is equal to 1000 m.


b.) The temperature outside an aircraft 1600 meters above Red Deer is -8.5 degrees Celsius. What is the temperature in the city?



b.) The answer is 1.9 degrees Celsius.
How did I get this? I added negative 8.5 and 10.4 degrees together and got 1.9.
How did I get 10.4? (0.65/100)x(1600)

It might not make sense, it was hard for me to explain it. Sorry, if it's late Mr. Backe. I was supposed to be done before 6 but the picture thing was'nt working properly. Like, whenever i upload my pics it doesn't show, it's just a small little box. There was just lot's of problems, I'm sorry it's okay if I get low marks.

9-05, the "CLASS" of 2009-2010

Heeeyyy 9-05 ! Do you guys remember one of our best students in class' post? Ahem DEAN ! If you forgot or didn't see it, it said something about us being "the class". I know Mr. Backe is proud of us because we are doing all our work and we are doing our job in the blog and everything else. Especially our daily commentors - Dean, Linda, Kara, Melissa, Joseph, sorry if I didn't mention your name... just tell me (: You guys are doing so great and for all the people who do their work all the time, going to our home page to check out Mr. Backe's assigned work and posting it for other people to see, you are doing awesome and keep it up! We are the "class" ! I was checking out the blog today and looking at all the post and I was just thinking that whoever sees it will be soo impressed because you guys did such a great job and keep it up and make Mr. Backe proud. This is our last year at Sargent and let's make it the best. Other classes are awesome too, 9-02,9-04 and 9-06. And again keep up the good work and let's keep on impressing people and making Mr. Backe proud. 9-05 FTW, going to be "THE CLASS" of 2009-2010. This is our year, let's make the best of it :D

Sincerely Yours, Karen (:

-you might think I'm a loser for doing this, I was bored so I decided to check out the whole blog and was so impressed with the things that I've seen and I wanted to pass out the message !

Scribe Post for October 20, 2009

HEEY 9-05 ! We didn't really do much today in class but do foldables for our new unit in math, Comparing and Ordering Rational Numbers. If you missed class today or didn't get the foldables done here it is: So, Backe gave us 6 pieces of paper, 2 big white one and 4 normal size blue ones. He asked us to fold them and do whatever it is in pg 44 in the math text book, mytextbook.ca.

Here is a picture of what it's supposed to look like, it's mine:

































How did I do this?
I used my big white piece of paper and folded it in threes equally. I took 2 pieces of blue paper and folded it in threes and then fold it in half and I folded the other 2 like a hotdog and glued it to the white paper.

After that, we had to fold the other whiter paper in threes and then fivided it in 6 sections like this:

*I know you can't really see this because it was too bright. It's supposed to be divided in 6 and you're supposed to write these words on each section/box and then the definition of the words behind that page and then numbers that belong and don't belong.
- Natural Numbers - Irrational Numbers
- Whole Numbers - Real Numbers
- Integers
- Rational Numbers

























I don't really know how to show you right but this is the best that I could. You put the numbers that don't belong at the back of numbers that belong.

I guess that's it. Don't forget to put the definitions, numbers that belong and don't belong again.

That's it! If I forgot something or made a mistake don't forget to point it out and don't forget to comment and tell me what I could've done better.
JOSEPH (JD!) you're next scribe. :D YOU'RE WELCOME!

9-05 commentors,
THANKS for all your comments and I changed the things that you told me to do so that it's better for you guys. (:

Rational Numbers

Heey 9-05! In case you guys don't know, Mr. Backé assigned us to post a blog about the term “Rational Numbers” mean and where it came from. Not that hard. Just search it online and type it here and publish. Oh, and you can also put a few examples. (:

Rational numbers are numbers capable of being expressed as an integer or a quotient of integers, excluding zero as a denominator.
e.g. 1.75 because it can be written as 7/4
0.001 because it can be written as 1/1000

Irrational numbers is a number that cannot be written as a simple fraction - the decimal goes on forever without repeating. It is called irrational because it can't be written as a ratio or fraction.
e.g. pi or π is irrational because the value is 3.1415926535897932384626433832795.....

Question #11

List places or situations in which surface area is important:

Buying a house or renting an area - apartment, space, etc.
*In case you need to know how big is the house or space. People usually needs to know the size of the rooms for them to pay for it and buy it.

Painting a room or a house.
*You need to know how much paint you're going to buy and use to paint whatever space you need to paint.

Buying a table.
*You first need the area of the space where you're going to put the table and then the area of the people so you know if it's going to fit in the space.

Buying carpet.
*You need the are of the space where you're going to put the carpet and how much carpet you will need to cover up the space.

Growing grass.
*If you're planning to grow grass in let's say your backyard with no grass at all and you want to cover it all. You have to know the area of your backyard to know how much grass you will have to put on it to cover it.

Building a house.
*You need to know the area of the lot (space where you're building the house)

Putting curtains or blinds.
* You need to know the area of the window you're going to cover and the (size length and width) of the blinds or curtains you need.

Tiling pools .or washrooms.
* You need to know the area of the washroom and the number of tiles you need.

Making a dress or any kinds of clothes for someone.
* You need to know the measurements of the person and the amount of fabric you will need.

Baking (brownies, cakes, etc.)
* You need to know the size of the pan, especially when your baking or making something that needs a baking pan. You need to know the size of the baking pan.

Building a pool.
*You need to know if the pool will actually fit and like how much you're going to dig for it to fit. You also need to know how much water you're going to put in the pool.

Wrapping presents.
*You need to know how much you're going to have to wrap and how much you need to cover it up.

When you're planning to decorate a space for a celebration.
*You need to know the area of the space you need to decorate to know how much decorations you need.

Watering plants.
*You need to know the size of whatever you're watering (for example: your lawn), you need to know how much water you need to water the whole thing.

Putting fertilizer on your plants.
*Just like watering your lawn. If you want to cover the whole lawn with fertilizer you have to know the size of your lawn to know how much fertilizer you need.

Road Trip.
*There are lots of examples here where you need to find area. First is the car, if you have lots of people and you are bringing lots of stuff with you, you need a car that will fit the car and to know how much stuff you can bring and how many people can go. Second, is the distance to where you are going.

Buying a cage or aquarium.
*You need to know the size and amount of animals you need to know what size of cage you're going to buy. You have to buy a cage that depends on how many pets you're going to put in it and the stuff that they need, like food and water bowl.

Elegant Algebraic Expressions

Heey everyone! This was an assignment from last week and I just found out about it this weekend. Sorry if it's late Mr. Backe. I haven't been on blogger for awhile so I'm not caught up with all the blogging assignments. Anyways, Mr. Backe asked us the find elegant algebraic expressions for the surface area of the following: cube, rectangular prism, cylinder, triangular prism and a composite of any of these shapes. He also wants us to answer these questions: How does symmetry help us solve some of these surface area problems? What happens if a part of any of these shapes is missing? How do I find surface area then? So here it goes....

Surface Area:

Cube
Finding the surface area of a cube is as easy as finding the area of a square and you just multiply it by 6 because there are six faces in a cube (six squares). Area formula for a square is: s x s or s squared.
Surface Area formula for a cube: 6s squared








Example: The side = 5.

SA= 6(5 squared)
SA= 6(25)
SA= 150 squared units.

Rectangular Prism
You only have to calculate 3 sides of a rectangular prism, lh+2lw+2wh, and multiply it by 2 because of symmetry.
Surface Area formula for a rectangular prism: 2(lh+2lw+2wh)






Example: The length = 5, width = 9 and the height = 4.

SA= 2(lh+2lw+2wh)
SA= 2(5)(4)+2(5)(9)+2(9)(4)
SA= 2(20)+2(45)+2(36)
SA= 40+90+72 SA= 202 squared units

Cylinder
To find the total surface area of a cylinder you first have to find the area of the two circles and then the area of the rectangle by multiplying the area of the circles to the height of the rectangle.
Surface Area formula for a cylinder: 2πr squared + 2πrh













Example: radius = 3 and height is = 9.

SA= 2πr squared + 2πrh
SA= 2π(3 squared) + 2π(3)(9)
SA= 2π(9) + 2π(27)
SA= 2(28.26) + 2(84.78)
SA= 56.52 + 169.56
SA= 226.08 squared units

Triangular Prism
Finding the surface area of a triangular prism seems hard but it's actually really easy. First you have to do the Pythagorean Theorem, a² + b² = c², then calculate the 2 triangles, 2(bh/2), then the sides or the "roofs", 2(h)(hyp), and then last but not least the bottom/ base, bh, and add it all up.
Surface Area formula for Triangular Prism: SA of base/bottom + SA of 2 triangles + SA of 2 roofs/sides











Example: height = 15, height of triangle = 6, and base is = 9.

2 Triangles
SA= 2(bh/2)
SA= (9)(6)
SA= 54 squared units

Base/Bottom
SA= bh
SA= (9)(15)
SA= 135 squared units

2 Roofs/Sides =(h)c²= a² + b²
hypotenuse
c²= a² + b²
c²= 4.5 squared + 6 squared
* How did I get 4.5? Divide the base, 9,by 2.
c²= 20.25 + 36
c²= 56.25 (square root)
c²= 7.5

whole roof
= 2(hyp)(h)
= 2(7.5)(15)
= 2(112.5)
= 225 squared units

Then add it all together...
SA= 1 base/bottom +2 triangles + 2 roofs/sides
SA= 135 + 54 +225
SA= 414 squared units

Composite
A composite figure is a figure (or shape) that can be divided into more than one of the basic figures. In other words, it`s a shape or a figure with more than one shape and it can also be divided. It can be a rectangular prism with another rectangular prism, smaller or bigger, a rectangular prism with a triangular prism so it looks like a house, a cube with another cube or it can be a rectangular prism missing a corner or a middle. To find the surface area of a composite figure you have to look for different surface areas of different objects and then add it all up or subtract it if there's a hole. You also have to subtract the area of the faces touching because it doesn't count because it's not showing.
Surface Area formula for this composite object: (SA of big rectangular prism + SA of small rectangular prism) - 2 (SA of one face of the small rectangular prism)









Example: (big rectangular prism) height = 4, length = 19 and width = 12. (small rectangular prism) height = 2, length = 10 and width = 5.

SA of big rectangular prism
= 2(lh+2lw+2wh)
= 2(19)(4)+2(19)(12)+2(12)(4) = 2(76)+2(228)+2(48) = 152+456+96
= 704 squared units

SA of small rectangular prism
= 2(lh+2lw+2wh)
= 2(10)(2)+2(10)(5)+2(5)(2)
= 2(20)+2(50)+2(10)
= 40+100+20
= 160 squared units

Area that is touching
= (lw)
= (10)(5)
= 50 squared units

Calculate...
SA formula for this composite object = (SA of big rectangular prism + SA of small rectangular prism) - 2 (SA of one face of the small rectangular prism)
= (704 + 160)- 2(50)
= (864)- 2(50)
= 864 - 100
= 764 squared units

How does symmetry help us solve some of these surface area problems? I think that symmetry helps us solve surface area problems easier. if you know where and what kind of symmetry an object, shape or figure has then it will be easier for us to solve and find the surface area. instead of calculating everything we can just multiply it by 2s, 4s, etc. depending on the symmetry it has. I don't know if that made sense and I'm sorry if I didn't.

What happens if a part of any of these shapes is missing? How do I find surface area then?
I don't really know how to explain this but I'm going to try my best. If a part of any of these shapes are missing you have to....
Look for the surface area of the whole thing and ignore the missing part for awhile then when you're done, find the surface area of the missing face and subtract that from the total surface area. That's what I would do. If that didn't make sense here's an example with a rectangular prism with no top:
Surface Area formula for a rectangular prism with no top part = SA of rectangular prism - SA of missing face/top part or 2(lh+2lw+2wh) - lw










Example: length = 10, width = 5 and height = 3.
SA = 2(lh+2lw+2wh) - lw
SA = 2(10)(3)+2(10)(5)+2(5)(3) - (10)(5)
SA = 2(30)+2(50)+2(15) - 50
SA = 60+100+30 - 50
SA = 140 squared units

Don't forget to comment! (; Tell me what you think about my post and point out my mistakes and everything. Sorry again if it's late ):

Why is a Circle 360 Degrees?

A circle is 360 degrees because....
the Babylonians used a base 60 number system. It seems clear that degrees were devised by ancient astronomers who noticed that the sun moved one degree each day (about our fixed Earth) past the stars that appeared to be fixed to an external heavenly sphere. It took one month for the sun to move the 30 degrees from one sign of the Zodiac to the next.

Since there are really 365 days in a year (not 360) why isn't a degree defined to be 1/365 of a circle instead of the official 1/360? I have seen several explanations, most not very convincing. My current favorite explanation is that the number 360 is a compromise between the solar year of about 365.25 days and the lunar year (consisting of 12 months of 29.5 days each) of about 354.37 days. Of course the months fit well with the Zodiac, which played an important role in their astronomy.

Sorry if this wasn't really that helpful, I got this from a site and this was the best one I got.
Source: http://mathcentral.uregina.ca/QQ/database/qq.09.96/kredo1.html