Elegant Algebraic Expressions

Hello everyone! I am making this blog post to show you the most elegant algebraic expressions for the surface area of a cube, rectangular prism, and a cylinder. I will also be answering some questions.

SURFACE AREA OF A CUBE = 6s²



S.A. = 6s²
S.A. = 6(2²)
S.A. = 6(2x2)
S.A. = 6(4)
S.A. = 24u²


SURFACE AREA OF A RECTANGLE = 2(lw)+2(lh)+2(hw)

S.A. = 2(lw)+2(lh)+2(hw)
S.A. = 2(5x6)+2(5x4)+2(6x4)
S.A. = 2(30)+2(20)+2(24)
S.A. = 60+40+48
S.A. = 148cm²

SURFACE AREA OF A CYLINDER = 2πr²+2πrh

S.A. = 2πr²+2πrh
S.A. = 2π(4²)+2π(4)h
S.A. = 2π(4x4)+2π(4)h
S.A. = 2π(16)+2π(4)
S.A. = 32π+8π
S.A. = 100.48+25.12
S.A. = 125.6cm²

COMPOSITE SHAPES
- a composite shape is a shape that can be divided into basic shapes, like a square, a rectangle, a triangle, etc.

This figure can be divided into two basic shapes, a triangle and a square.

HOW DOES SYMMETRY HELP US SOLVE SOME OF THESE SURFACE AREA PROBLEMS?
It helps us solve some of these area problems because some of the shapes have symmetry. Some shapes have sides that are the same, like, a square. all 6 sides have identical sides. If we know that there it has identical sides, then we can form a formula to solve the surface area of the shape.

WHAT HAPPENS IF A PART OF ANY OF THESE SHAPES IS MISSING? HOW DO I FIND SURFACE AREA THEN?
If there was a part missing in any of these shapes, you would have to calculate the missing area, and subtract it from the original shape.

THANK YOU FOR READING MY BLOG POST ! (: I hope this helps you learn more about surface area and please feel free to comment if I made any mistakes.

Elegant Algebraic Expressions

First of all.. I'd like to say HAPPY THANKSGIVING/TURKEY DAY to everyone! (: Okay so this blog post will be about the most elegant algebraic expressions to help you find the surface area for a cube, a rectangular prism, a cylinder, and a composite shape. So let's start! :D


What is the most elegant algebraic expression for a cube?
The most elegant algebraic expression for a cube is 6s².

So now, we'll use a 2 by 2 cube for an example to find the surface area.















This is how you find the surface area for a cube: S.A. of cube = 6s²
S.A. of cube = 6(2²)
S.A. of cube = 6(4)
S.A. of cube = 24u²


What is the most elegant algebraic expression for a rectangular prism?
The most elegant algebraic expression for a rectangular prism is 2(lw)+2(hw)+2(lw).

For an example, we'll use a rectangular prism with a length of 5, a width of8, and a height of4.















This is how you find the surface area for a rectangular prism:
S.A. of rectangular prism = 2(lw)+2(hw)+2(lw)
S.A. of rectangular prism = 2(5x8)+2(4x8)+2(5x8)
S.A. of rectangular prism = 2(40)+2(32)+2(40)
S.A. of rectangular prism = 80+64+80
S.A. of rectangular prism = 224cm²


What is the most elegant algebraic expression for a cylinder?
The most elegant algebraic expression for a cylinder is 2πr²+2πrh.

To show how to find the surface area of a cylinder, we'll use a cylinder with a diameter of 10 and a height of 15.














This is how you find the surface area for a cylinder:
d/2 = r
10/2 = r
5 = r

S.A. of cylinder = 2πr²+2πrh
S.A. of cylinder = 2π5²+2π5(15)
S.A. of cylinder = 2π25+2π75
S.A. of cylinder = 50π+150π
S.A. of cylinder = 157.079+471.238
S.A. of cylinder = 628.317u²

What is a composite figure?
A composite figure is a figure or shape that can be divided into more than one of the basic figures.

Here is an example of a composite figure:
This figure is divided into two squares and triangles, which are basic shapes.










How does symmetry help us solve some of these surface area problems?
Symmetry helps us solve these surface area problems because if you know a shape has symmetry you would that it is balanced. Like a rectangle.. it's front is the same as it's back, and so as the 2 sides and the top and bottom. I'm not sure if I made sense here though.

OKAY.. So I hope this blog post helped anyone who needed help! If there's anything missing, or if there's any errors, don't be afraid to comment~! Have a good Thanksgiving/Turkey Day you guys and I'll see you tomorrow~!

Elegant Algabraic Expressions

Hi 9-05! Mr. B has assigned us all some homework for the weekend. We're supposed to answer a few questions about surface area, so I'm going to answer mine in the most blunt way possible.

WHAT IS THE MOST ELEGANT ALGEBRAIC EXPRESSION FOR ...

... surface area of a cube?

Well, you see, a cube has 6 faces and each of those 6 faces are equal. Since each of those faces are equal, whatever length one side is would be squared.

i.e. 3 by 3 cube

The most elegant algebraic expression for a cube would be 6s²

Example:
SA= 6s²

SA= 6(3²)
SA= 6(9)
SA= 54u²

... surface area of a rectangular prism?
Being a prism, a rectangular prism has 6 faces. Although, unlike a cube, a rectangular prism does not have all equal sides. A particularly good way to see how to calculate surface area of a rectangular prism wold be to see how its net looks like.

Seeing the measurements is a good way of seeing what parts of the rectangular prism have plane symmetry. The net above, however, is not the only way to portray the net of a rectangular prism. It's actually kind of confusing, but the picture itself is quite clear.

The most elegant algebraic expression for a rectangular prism is SA= 2(lw) + 2(hw) + 2(hl)

Example:

h=5

l=4

w=2

SA= 2(lw) + 2(hw) + 2(hl)

SA= 2(4)(2) + 2(5)(2) + 2(5)(4)

SA= 2(8) + 2(10) 2(20)

SA= 16 + 20 + 40

SA= 76u²

*remember to always add in the u² after your answer because we're dealing with 3D shapes

... surface area of a cylinder?

I'm sure all of you are familiar with how we learned this formula last year, where we just found the area of the two circles and the rectangle of the cylinder and added them all together. As you all should know, we learned a different way to calculate surface area of a cylinder.

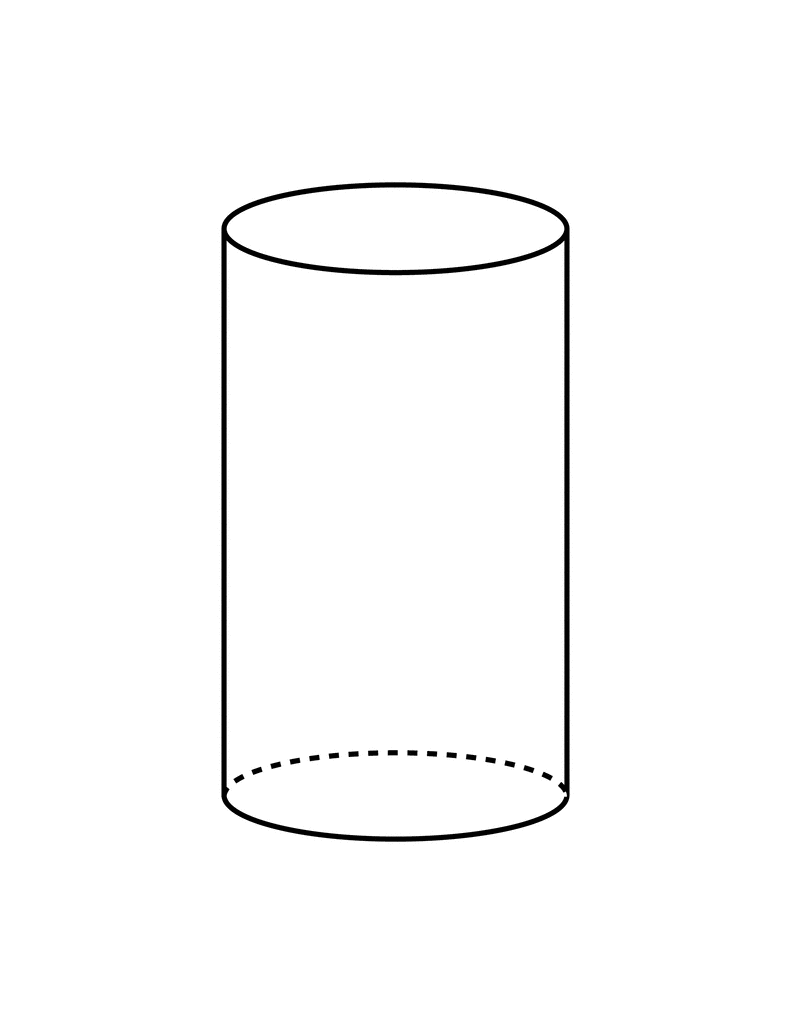
During one of our math classes we learned that the circumference of the circle of the cylinder is equal to the width of its rectangle. To test this out just roll up a rectangular peice of paper and look at the circle and see that its width goes all around the circle, or rather the circumference.

Since we're calculating surface area of a cylinder, we know we need to have the formula for area of two circles. The formula for a circle is πr², so the formula for two circles would simply be 2(πr²). Now we need to find the area of the rectangle of the cylinder. We know that the width is equal to the circumference of the circle, and area of a rectangle is (lw) so we multiply 2πr by height, which is like the length of a rectangle.

So the most elegant algebraic expression for a cylinder is SA= 2(πr²) + 2πrh

COMPOSITE SHAPES
I actually didn't know what a composite shape was at first, but I found that it's a figure that can be divided into two or more shapes. This was what Mr. B has been telling us about for the past couple of days, but I didn't know what the technical term was then.
I think the best way to calculate the surface area for composite shapes is to look at the figure from all angles and add it all up because this can apply to all composite shapes. Some composite shapes have holes and spaces in them and this can make calculating surface area for composite shapes confusing.

HOW DOES SYMMETRY HELP US SOLVE SOME OF THESE SURFACE AREA PROBLEMS?
A figure usually has 6 faces; 3 sets of 2 symmetrical faces. Plane of symmetry are imaginary lines drawn on polyhedrons to show that both sides are symmetrical. Imagine these lines as if they cut right through the polyhedron. Symmetry helps us solve for surface area because if we see one face we know that on the opposite side there should be another face just like it. This rule usually applies for regular shapes, however. Understanding symmetry allows us to see that if one side has a measurement of so-and-so, then the other side should have that same length as well.

WHAT HAPPENS IF A PART OF ANY OF THESE SHAPES IS MISSING? HOW DO I FIND SURFACE AREA THEN?

Most polyhedrons usually have plane of symmetry. We can use plane of symmetry to find the missing part of a shape by finding its symmetrical other.

Example of Plane of Symmetry:

I hope in one way or another this has helped! Please feel free to comment! :)