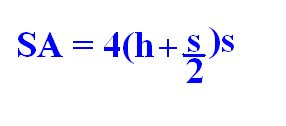Elegant Algebraic Formulas

Hi, again... this is going to be my second post for today and it's going to be about the most "Elegant Algebraic Formulas" to use for finding the surface areas for certain shapes.

The most elegant algebraic formula for find the cube's surface area is S.A=6s², because there are 6 faces and each side is a certain measurement.

The best or I mean the most elegant algebraic formula for finding the Surface area for the Rectangular Prism is in the picture below..

And Finally the elegant algebraic formula for finding the Surface area for the Cylinder is again, located in the picture below...

Elegant Algebraic Equations

Elegant Algebraic equations.

I didn't know what Mr. Backe was talking about when he said Elegant Algebraic Equations. And thats what they are, the most elegant way to find the surface area of a shape. So im going to tell you the different formulas for different shapes.

S.A of a Cube 6s²

Say the cubes side lenght is 7

S.A 6s²

S.A = 6(7²)

S.A = 6(49)

S.A= 294 u²

A rectangular Prism

S.A 2(lw)+ 2(hw) + 2(hl)

S.A 2 (4)(6) + 2 (5)(6) + 2(5)(4)

S.A 2 (24)+ 2(30)+ 2(20)

S.A 48+ 60+40

S.A 148u²

Cylinder

S.A 2pi r² + 2 pi rh

S.A 2 (3.14)(5²) + 2(3.14)(5)(20)

S.A 2(3.14)(25)+ 2(3.14)(100)

S.A 2 (78.539) + 2 (314.159)

S.A 157.078 + 628.318

S.A 785.396 u²

Triangular Prism

2 Triangles bh ( don't put divided by 2 because bh/2 is for one triangle I am finding for 2)

2 triangles (15)(10)

2 triangles 150u²

base of prism lw

base of prism (15)(20)

base of prism 300u²

2 roofs lw

first we need the side of the roof.

a² + b² = c²

10²+ 15²=c²

100+ 225 = c²

(sqroot)325= (sqroot)c²

18.027 = c

2 roofs lw

2 roofs (20) (18.027)

2 roofs 360.555 u²

Add everything together.

150u² + 300u² + 360.555 u²=

810.555u²

Elegant Algebraic Expressions

Heey everyone! This was an assignment from last week and I just found out about it this weekend. Sorry if it's late Mr. Backe. I haven't been on blogger for awhile so I'm not caught up with all the blogging assignments. Anyways, Mr. Backe asked us the find elegant algebraic expressions for the surface area of the following: cube, rectangular prism, cylinder, triangular prism and a composite of any of these shapes. He also wants us to answer these questions: How does symmetry help us solve some of these surface area problems? What happens if a part of any of these shapes is missing? How do I find surface area then? So here it goes....

Surface Area:

Cube
Finding the surface area of a cube is as easy as finding the area of a square and you just multiply it by 6 because there are six faces in a cube (six squares). Area formula for a square is: s x s or s squared.
Surface Area formula for a cube: 6s squared








Example: The side = 5.

SA= 6(5 squared)
SA= 6(25)
SA= 150 squared units.

Rectangular Prism
You only have to calculate 3 sides of a rectangular prism, lh+2lw+2wh, and multiply it by 2 because of symmetry.
Surface Area formula for a rectangular prism: 2(lh+2lw+2wh)






Example: The length = 5, width = 9 and the height = 4.

SA= 2(lh+2lw+2wh)
SA= 2(5)(4)+2(5)(9)+2(9)(4)
SA= 2(20)+2(45)+2(36)
SA= 40+90+72 SA= 202 squared units

Cylinder
To find the total surface area of a cylinder you first have to find the area of the two circles and then the area of the rectangle by multiplying the area of the circles to the height of the rectangle.
Surface Area formula for a cylinder: 2πr squared + 2πrh













Example: radius = 3 and height is = 9.

SA= 2πr squared + 2πrh
SA= 2π(3 squared) + 2π(3)(9)
SA= 2π(9) + 2π(27)
SA= 2(28.26) + 2(84.78)
SA= 56.52 + 169.56
SA= 226.08 squared units

Triangular Prism
Finding the surface area of a triangular prism seems hard but it's actually really easy. First you have to do the Pythagorean Theorem, a² + b² = c², then calculate the 2 triangles, 2(bh/2), then the sides or the "roofs", 2(h)(hyp), and then last but not least the bottom/ base, bh, and add it all up.
Surface Area formula for Triangular Prism: SA of base/bottom + SA of 2 triangles + SA of 2 roofs/sides











Example: height = 15, height of triangle = 6, and base is = 9.

2 Triangles
SA= 2(bh/2)
SA= (9)(6)
SA= 54 squared units

Base/Bottom
SA= bh
SA= (9)(15)
SA= 135 squared units

2 Roofs/Sides =(h)c²= a² + b²
hypotenuse
c²= a² + b²
c²= 4.5 squared + 6 squared
* How did I get 4.5? Divide the base, 9,by 2.
c²= 20.25 + 36
c²= 56.25 (square root)
c²= 7.5

whole roof
= 2(hyp)(h)
= 2(7.5)(15)
= 2(112.5)
= 225 squared units

Then add it all together...
SA= 1 base/bottom +2 triangles + 2 roofs/sides
SA= 135 + 54 +225
SA= 414 squared units

Composite
A composite figure is a figure (or shape) that can be divided into more than one of the basic figures. In other words, it`s a shape or a figure with more than one shape and it can also be divided. It can be a rectangular prism with another rectangular prism, smaller or bigger, a rectangular prism with a triangular prism so it looks like a house, a cube with another cube or it can be a rectangular prism missing a corner or a middle. To find the surface area of a composite figure you have to look for different surface areas of different objects and then add it all up or subtract it if there's a hole. You also have to subtract the area of the faces touching because it doesn't count because it's not showing.
Surface Area formula for this composite object: (SA of big rectangular prism + SA of small rectangular prism) - 2 (SA of one face of the small rectangular prism)









Example: (big rectangular prism) height = 4, length = 19 and width = 12. (small rectangular prism) height = 2, length = 10 and width = 5.

SA of big rectangular prism
= 2(lh+2lw+2wh)
= 2(19)(4)+2(19)(12)+2(12)(4) = 2(76)+2(228)+2(48) = 152+456+96
= 704 squared units

SA of small rectangular prism
= 2(lh+2lw+2wh)
= 2(10)(2)+2(10)(5)+2(5)(2)
= 2(20)+2(50)+2(10)
= 40+100+20
= 160 squared units

Area that is touching
= (lw)
= (10)(5)
= 50 squared units

Calculate...
SA formula for this composite object = (SA of big rectangular prism + SA of small rectangular prism) - 2 (SA of one face of the small rectangular prism)
= (704 + 160)- 2(50)
= (864)- 2(50)
= 864 - 100
= 764 squared units

How does symmetry help us solve some of these surface area problems? I think that symmetry helps us solve surface area problems easier. if you know where and what kind of symmetry an object, shape or figure has then it will be easier for us to solve and find the surface area. instead of calculating everything we can just multiply it by 2s, 4s, etc. depending on the symmetry it has. I don't know if that made sense and I'm sorry if I didn't.

What happens if a part of any of these shapes is missing? How do I find surface area then?
I don't really know how to explain this but I'm going to try my best. If a part of any of these shapes are missing you have to....
Look for the surface area of the whole thing and ignore the missing part for awhile then when you're done, find the surface area of the missing face and subtract that from the total surface area. That's what I would do. If that didn't make sense here's an example with a rectangular prism with no top:
Surface Area formula for a rectangular prism with no top part = SA of rectangular prism - SA of missing face/top part or 2(lh+2lw+2wh) - lw










Example: length = 10, width = 5 and height = 3.
SA = 2(lh+2lw+2wh) - lw
SA = 2(10)(3)+2(10)(5)+2(5)(3) - (10)(5)
SA = 2(30)+2(50)+2(15) - 50
SA = 60+100+30 - 50
SA = 140 squared units

Don't forget to comment! (; Tell me what you think about my post and point out my mistakes and everything. Sorry again if it's late ):

Elegant Algebraic Expressions for Finding Surface Area

I always wonder why we use those "elegant" algebraic expressions in math class. Well, I could probably answer my own questions. We use those formulas because, it's easier to understand (I think..) and when we write it out, it looks elegant, or beautiful, or whatever. I also think that we use those formulas because, mathematicians use it. We want to be like them!!!! :D

So, I'm here to blog about what formulas/ algebraic expressions are elegant for different kinds of shapes. Also to give examples on how to use them.


What is the most elegant algebraic expression...

for finding the surface area of a cube?

-A cube simply has 6 faces that are equal, so whatever length on one side is squared.

To find the surface area of a cube, you simply use this formula:


S.A.= 6s²

Just for an example on how to use that formula, I will find the surface area of the cube with a side length of 5.


S.A.= 6s²

= 6 (5²)

= 6 (25)

S.A.=150 u²

What is the most algebraic expression...


for finding the surface area of a rectangular prism?

-We already learned this last year, so I think you're familiar with the formula. A rectangular prism has 3 sets of 2 equal faces (each set), that equals to 6 faces in total.


In finding the surface area of a rectangular prism, you could use this formula:

S.A.+ 2(lw)+2 (hw)+ 2 (hl)



For example on how to use that formula for finding the surface area of a rectangular prism, I will use it, using the measurements shown above (in the picture).


S.A.= 2 (lw)+ 2 (hw)+ 2 (hl)

= 2 (7) (4) + 2 (10) (4) +2 (10) (7)

= 2 (28) + 2 (40) + 2 (70)

=56+80+140

S.A. = 276 cm²

* NEVER forget to put the unit (eg. cm)/ measurement and the squared sign (²) in your answers.

What is the most elegant algebraic expression...


for finding the surface area of a cylinder?


-We already learned this last year too. So, you're most likely to know this formula. You have to find the surface area of the 2 circles, then add the rectangle. The find the surface area of the rectangle, you multiple the height by the circumference of the circle.


To find the surface area of a cylinder, you use this formula:


S.A. = 2πr²+ 2πrh








I'm going to use the measurements above, in giving an example on how to use the formula.


S.A.=2πr²+2πrh

=2(3.14)(5²)+2(3.14)(5)(15)

= 2 (3.14) (25)+ 2 (3.14) (75)

= 2 (78.54)+2 (235.62)

= 157.08+ 471.24

S.A.= 628.32cm²


What is the most elegant algebraic expression...

in finding the surface area of a triangular prism?



-Triangular prisms also uses formulas. But, it's kind of mixed. You have to use the Pythagorean theorem, the formula for finding the area of the triangles, and finally, the formula for finding the area of a rectangle.





Area of 2 triangles= bh

= (10)(15)

= 150




Area of base= lw

= (10)(20)

= 200

*For finding the area of the roofs, most of the time, only one side is given. So you use the Pythagorean theorem to find the hypotenuse of the triangle, which is the unknown side. Then you multiply that by the side that is given (width).




a²+b²= c²

10²+15²=c²

100+225=c²

325=c²

√325=√c²

18.03=c





Area of 2 rectangles (roofs) = 2(lw)

= 2(18.03)(20)

= 2(360.55)

=721.11

Then, you add all of the areas together, to get the total surface area.

S.A.=Area of triangles+Area of base+Area of roofs

=150+200+721.11

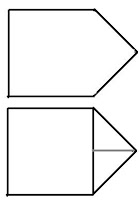
=1071.11


What is the most elegant algebraic expression...



in finding the surface area of a composite object?


- There's no formula to use in particular. It all depends on what shapes are combined.

In this particular shape, I would use the formula for finding the surface area of a rectangular prism. I would have to use that twice (top and bottom). Add them together. Then, find the area of the overlap, then subtract.

S.A. (bottom)= 2(lw)+2 (hw)+ 2(hl)

= 2 (5)(2) + 2 (2)(2)+ 2 (2)(5)

= 2 (10)+2 (4)+ 2 (10)

= 20+8+20

= 48

S.A. (top)= 2(lw)+2(hw)+2(hl)

= 2(5)(1)+2 (2)(1)+2(2)(5)

= 2(5)+2(2)+2(10)

= 10+ 4+ 20

= 34

Area of overlap = (1)(5)(1)

= 5

S.A.=area (bottom)+ area (top) -area of overlap

=48+34-5

S.A. =77 u²

How does symmetry help us solve some of these surface area problems?

- Well, that's an interesting question. It's also an easy question to answer. Most solid shapes (eg. rectangular prism) has planes of symmetry in it. Planes of symmetry helps us how many faces are equal. Which helps us to know that when we see one side of that shape, the opposite side is the same. Planes of symmetry only applies to some shapes. So, it can't be like that for every shape.

What happens when a part of any of these shapes is missing? How do I find the surface area then?

-Simple! Most shapes have planes of symmetry. So if one side is missing, you will know that it's the same as the given part. That helps on finding the missing part of a shape, then calculating the surface area with the missing shape.

Hey! Feel free to comment on how great this post is! Also feel free to criticize this post! Or just comment! :D

Most Elegant Algebraic Expressions

Hello everyone! I'm sorry I couldn't go on for a few days, my Internet wasn't working properly. Finally it's working. So now I can do the posts Mr. Backe assigned us. And I can finally comment too. So anyways I am going to tell you the Most Elegant ways to find Rectangular Prisms, Triangular Prisms, the Cube, the Cylinder, and any Square Based Prism.

The Rectangular Prism:

SA=2(lw)+2(hl)+2(hw)

SA=2(6)(10)+2(4)(10)+2(4)(6)

SA=120+80+48

SA=248 square units

The Triangular Prisms:

First you find the area of a triangle.

A=bh/2

A=(4)(4)/2

A=16/b

A=8 square units

And then the base.

A=bh

A=(4)(10)

A=40 square units

And finally the roofs.

You have to find the hypotenuse by using the Pythagorean Theorem.

a squared + b squared = c squared

4 squared + 4 squared = c squared

16 + 16 = c squared

32 (square rooted) = c squared (square rooted)

5.656 = c

A=2[h(Hyp.)]

A=2[10(5.656)]

A=2(56.56)

A=113.12 square units

Then you add all of the answers together.

113.12 + 40 + 8 = 161.12 square units

I know it looks complicated but this is as elegant it's gonna get.

The Cube:

SA= 6s squared

SA= 6(3) squared

SA= 6(9)

SA= 54 units square

The Cylinder:

SA=2 pi r squared + 2 pi r h

SA=2(3.14)(3)squared + 2 (3.14)(3)(8)

SA=2(3.14)(9) + 2(3.14)(24)

SA=(3.14)18+ (3.14) 48

SA=56.52+150.72

SA=207.24

Any Square Based Prism:

You could use this if you have any Prism with a square. You could use it as a base. If you had a rectangular prism with a square on the sides than you use this formula.

Thank you for reading! Please leave a comment and tell me how I did!

The Most Elegant Algebraic Formulas

Happy Thanksgiving to everyone!

The most elegant formula to find the total surface area of a cube is TSA=6s². That's basicly saying the length of one side squared, multiplied by 6 (because there are 6 faces on a cube).

Eg.

TSA= 6s²

TSA=6(2²)

TSA=6(4)

TSA=24u²

The most elegant formula to use when finding the TSA of a rectangular prism is
TSA=2(=lw+hl+hw). Luckily you only have to find the area of 3 different sides, thanks to symmetry. When you know one side, you know the opposite side. (Only for Rectangular Prisms)

Eg.

TSA=2(lw+hl+hw)
TSA=2(4x2 + 6x4 + 6x2)

TSA=2(8+24+12)

TSA=2(42)

TSA=84u²

The most elegant formula to find the toal surface area of a cylinder would be TSA=2πr²+2πrh.
2πr² is to find the to circle shaped tops of a cylinder. Then when you add the 2πrh, it's the area of the rectagular net (tube of cylinder). h is the height of the cylinder. 2πr is to find the circumference. (2r x π is equal to πd).

Eg.

TSA=2πr²+2πrh
TSA=2(3.14)(2²)+2(3.14)(2)(10)

TSA=2(3.14)(4)+2(3.14)(2)(10)

TSA=25.12+125.6

TSA=150.72u²

Finally, time for the total surface area of a composite. Sadly, there is no certain formula for TSA's of composite figures. That's only because composite shapes are all different. A composite shape is one big shape made by combining little basic shapes. To find the TSA for these typesof shapes, simply cut the shape into the basic shapes, and then REMEMBER to subtract the area of overlap, from both shapes connecting. (for 3D shapes)

Eg.

O___O What's that shape?....if you think about it, you can turn it into a square and two right angle triangles. Let's give side length of the square 5 and length a (verticle) of the triangle=2.5, with b=6. Usually you would need to find length "c", but since there are two symmetrical triangles it will make a rectangle. So that means you find the area of a square and a rectangle with the dimensions of a triangle.

Area of square= s²

Area of square= 5²

Area of square= 25u²

Area of Rectangle=lw

Area of Rectangle=2.5x6

Area of Rectangle=15u²

TSA=40u²